[Paper] Batch Normalization
Abstract
Deep neural network 를 trainig 할 때, 이전 계층의 parameter가 변화함에 따라 각 게층의 입력 분포가 변경되는점 때문에 낮은 learning rate 와 parameter initialization시에 조심해야 하기 때문에 training 속도가 낮아지고 non-linearity 를 가진 모델 trianing이 매우 어렵다.
이러한 현상을 internal covariate shift라 하며, layer input에 normalization을 적용 하여 문제를 해결한다.
이 논문에서는 normalization을 model architecture의 일부로 만들고 각 training mini-batch에 대한 normalization을 수행한다.
Batch Normalization은 더 높은 learning rate를 사용하고 parameter initialization에 있어 주의를 완화해준다.
또한 Regularizer로도 작용하여, 몇몇 case에서는 Dropout이 필요하지 않다.
Introduction
SGD는 network의 parameter Θ 를 최적화하여 loss를 최소화한다.
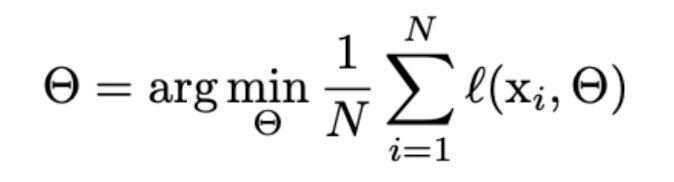
- x1…xn : training data set
- training이 단게별로 진행되며, 크기 m의 mini batch를 고려한다.
- mini batch는 다음 계산식을 통해 loss function의 gradient를 근사화 하는데 사용한다.
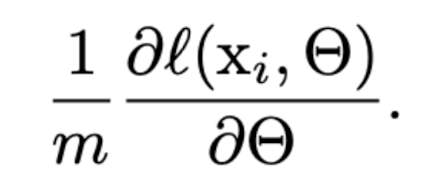
SGD의 mini batch 사용의 장점
- mini batch에 대한 loss의 gradient는 training set에 대한 gradient의 추정치이다. batch size가 커질수록 전체 데이터를 추정하는 것이 정교해진다.
- 컴퓨터가 발전함에 따라 병렬 처리로 인해 계산이 훨씬 빨라진다.
SGD의 단점
- hyper parameter 초기화 시 주의해야한다.(특히 learning rate)
- network가 깊어질수록 이전 layer가 다음 layer에 영향을 끼침에 따라 Gradient Vanishing/Explode 가 나타날 수 있다.
Covariate shift(공변량 이동)
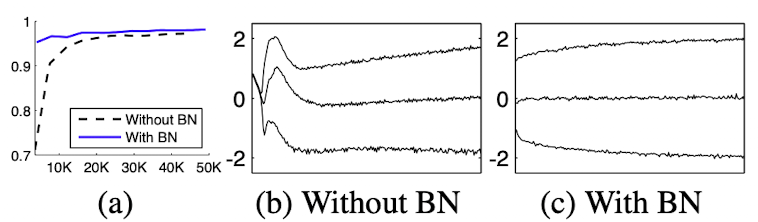
- layer에 들어가는 input의 분포가 바뀌게 되면 모델 내의 parameter들은 새로운 분포에 대해 다시 적응하고 학습해야 하는데, 이 때의 train과 test data의 입력 분포의 차이를 covariate shift 라 한다.
- 이를 제거하면 더 빠른 training이 가능하다.
- 사진은 MNIST dataset에서의 실험
- b,c : sigmoid에 대한 입력 분포의 진화
Batch Normalization은 internal covariate shift를 제거하여 학습 속도를 향상시키고, 모델을 정규화 하고 Dropout의 필요성을 줄였다.
Towards Reducing Internal Covariate shift
Whitening
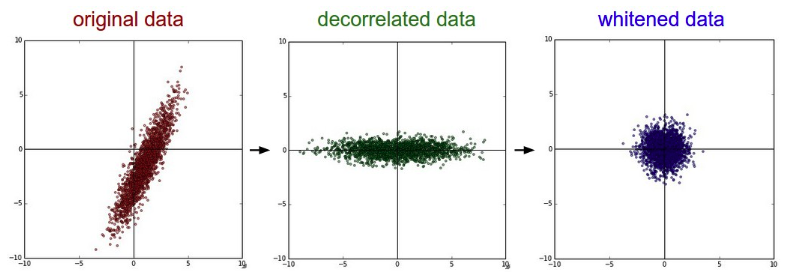
- 각 layer의 입력의 분산을 평균 : 0, 표준편차 : 1 인 입력값으로 정규화 시키는 방법. 입력값의 특징들을 uncorrelated 하게 만들어준다.
문제점
- covariance matrix 와 inverse 계산이 필요하기 때문에 계산량이 많다.
- 일부 parameter의 영향이 무시되어 gradient descent 효과를 감소시킨다.
- ex)input = u,learned bias = b,x hat = x - E[x],x = u + b,X = {x1,..,xn}(training set),E[x] = x의 평균
- x hat에서 평균값을 빼주는 과정에서, b도 같이 빠지게 되어 출력에서 b의 영향이 사라진다.
- 이로 인해 loss가 변하지 않으면 gradient가 한없이 커진다.
이는 gradient descent optimitzation이 정규화를 고려하지 않기 때문에 일어나는 문제점으로, 어떤 parameter를 사용하더라도 네트워크의 출력들이 고안된 분포를 따르도록 해주어야 한다.
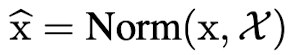
- x : layer input vector
- X: 전체 dataset의 모든 input vector
- x,X로 표현한 정규화
backpropagation을 위해서, Jacobian을 구해야한다(다변수 함수)
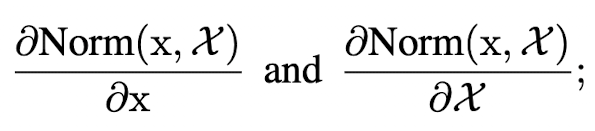
- x,X 둘 다 정규화 과정에 포함
이 계산과정까지 거치게 된다면 새로운 covariate matrix와 inverse square root를 계산해야 하기 떄문에 계산량이 많아져 비효율적이다.
때문에 다음 2가지 조건을 만족하는 새로운 방법을 찾았다.
- 미분 가능한 연산
- parameter 업데이트 시 전체 데이터에 대한 연산을 요구하지 않음
Normalization via Mini-batch Statistics
간소화 과정
첫번째 방법
- input data의 각 scalar 값인 차원에 대해 독립적으로 정규화
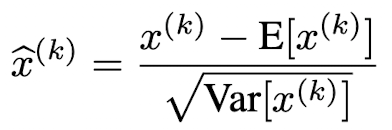
- 이 때 E[x] 와 Var[x] 는 training data 각 차원에 대해 계산
장점
- feature가 decorrelated 되지 않았어도 수렴 속도가 높아진다.
단점
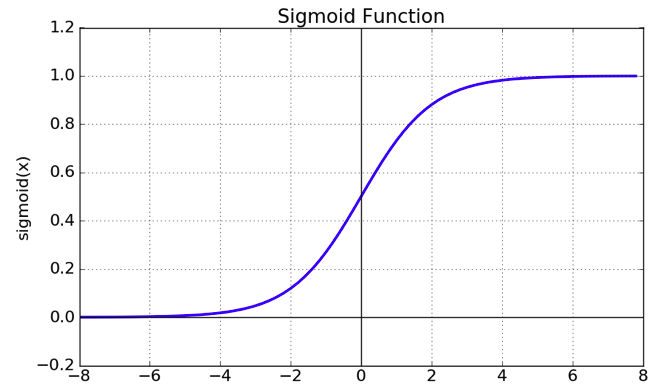
- 정규화를 통해 각 차원의 scalar 값이 평균이 0이고 표준편차가 1인 분포를 따르게 되었다.
- activation function으로 sigmoid 사용시, sigmoid 함수의 [-1,1] 구간에서는 거의 직선에 수렴하기 때문에, non-linearity를 잃게 된다.
- 이 문제를 해결하기 위해 각 차원마다 γ 와 β를 도입하여 scaling과 shifting을 통해 해결한다.
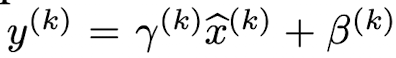
두번째 방법
- 정규화 시 batch를 사용한 학습에서는 전체 데이터에 대한 평균과 분산 값을 구하는 것이 불가능하기 때문에 배치에 대한 평균과 분산값을 통해 정규화를 진행해야 한다.

Batch Normalization
- 평균과 분산을 조정하는 과정이 신경망 안에 포함되어 학습 시 평균과 분산을 조정하는 과정이 같이 조절된다.
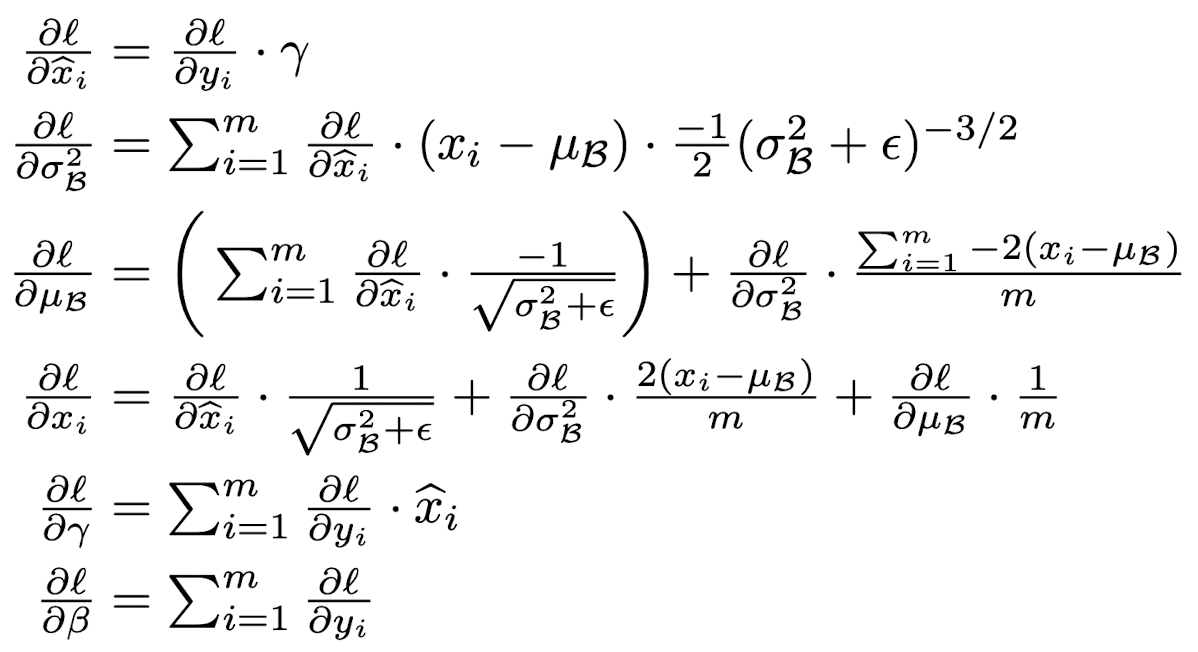
- 정규화된 값 -> activation function의 입력
- 최종 출력 값 -> 다음 layer 입력
Training and Inference with Batch-Normalized Networks
- training 시에는 Batch Normalization의 mini batch의 평균과 분산을 이용할 수 있지만, inference 및 test시에는 이를 사용할 수 없다.
- 모델이 학습되는 동안 추정한 입력 데이터의 평균과 분산으로 정규화를 해야 하는데, inference시에 입력되는 값을 통해 정규화를 하게 되면 모델이 학습을 통해 입력 데이터의 분포를 추정하는 의미 자체가 없어지게 된다.
- 때문에 inference시에는 고정된 평균과 분산을 사용하여 정규화를 수행하게 된다.(train,test변경시 on/off)
Moving Average

- inference 전에 학습 시에 미리 mini batch를 뽑을 때 sample mean과 sample variance를 이용하여 각각의 Moving Average를 구해야 한다.
- 위 수식의 6~12번 에서는 평균은 mini batch에서 구한 평균들의 평균을 사용하고, 분산은 분산의 평균에 m/(m-1)를 곱해준다. 이는 Bessel’s correction 때문이라고 하는데 이 부분은 아직 잘 모르겠다.
Batch-Normalized Convolutional Net-works
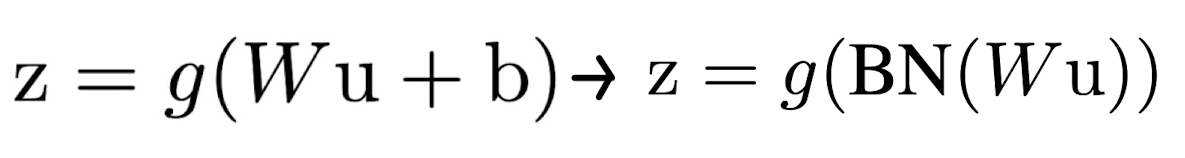
-
CNN layer에서 activation function 전에 WX + b로 가중치가 적용되었을 떄, b의 역할을 β가 대신 해주기 때문에 b를 생략한다.
- Convolution 성질을 유지하고 싶기 때문에 각 채널을 기준으로 각각 γ 와 β를 만든다.
- Convolution kernel 하나는 같은 γ 와 β를 공유하게 된다.
