[Paper] Layer_Normalization

Abstract & Introduction

SOTA model을 훈련시킬때, deep neural network들은 계산 시 비용이 많이 든다. 이러한 training 시간을 줄이는 방법중 하나는 뉴런들의 activity 를 정규화 하는 것이다.

최근에 알려진 Batch Normalization은 mini-batch의 크기에 영향을 받고, RNN에서는 어떻게 적용되어야 하는지 알려지지 않았다.

이 논문에서는 하나의 training case에서, layer 의 뉴런에 대한 모든 summed input의 정규화에 사용되는 mean, variance를 계산함으로써 Batch Normalization 을 Layer Normalization으로 바꾼다.

• 공통점
  • normalization과 비선형 회귀 사이에 뉴런 각각에게 adaptive bias 와 gain을 준다.
• Layer Normalization의 차이점
  • Layer Normalization은 Training 과 test에서 완전히 같은 계산 비용과 시간을 보여준다.
  • RNN의 은닉층을 안정화 시키는데 효과적이다.

RNN은 Feed forward network와 달리 input의 길이가 다르기 때문에 Time-step에 따라 다른 통계를 써야하기 때문에, Batch Normalization은 사용할 수 없지만 Layer Normalization은 각 Time-step마다 normalization 통계를 계산하기 때문에 RNN에 적용할 수 있다.

Layer Normalization

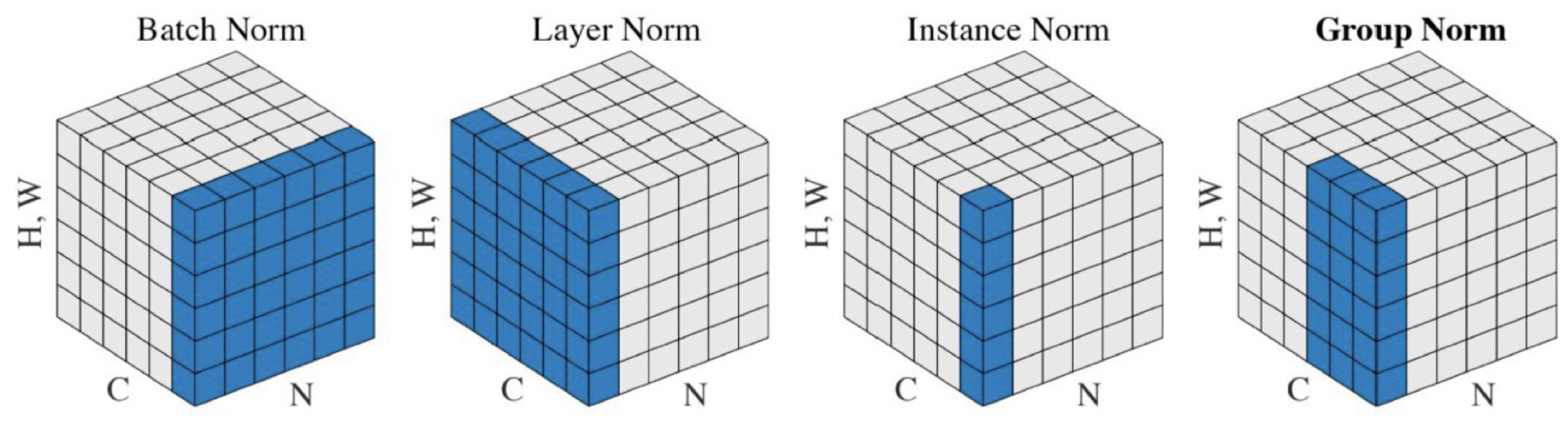
• 각 training case 별로, 한 mini-batch에 대한 summed input의 평균과 분산을 구한다.
• 각 input의 feature들에 대한 평균과 분산을 구해 각 층의 input을 정규화한다.

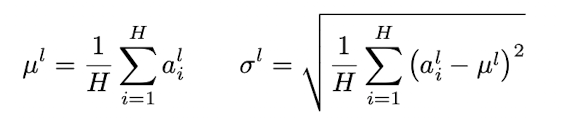
• ali : l번째 layer의 i번째 hidden unit으로 들어가는 input 총합(바 가 붙을 시 정규화 값).
• μ : 평균
• σ : 표준편차
• H : layer의 hidden unit의 수
• Layer Normalization에서는 같은 layer에 있는 모든 hidden unit들이 평균과 표준편차(정규화 통계량) 을 공유한다. 하지만 다른 training case들은 다른 정규화 통계량을 가진다.
• Batch Normalization과는 다르게 mini-batch 사이즈에 영향을 받지 않아 하나의 객체에 대해서도 정규화를 할 수 있다.

Layer nomalized recurrent neural network

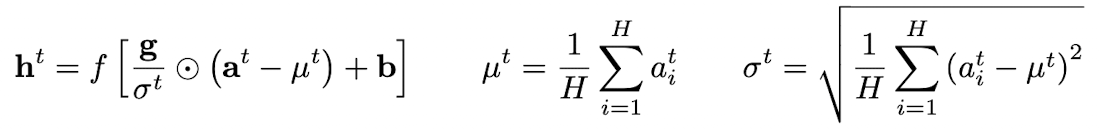
• RNN 에서의 정규화

NLP 문제에서는 training case마다 문장 길이가 다른 경우가 많은데, RNN에서는 모든 time-step에서 같은 weight를 사용하기 때문에 이러한 문제에 효과적이다.

• Batch Normalization의 문제점
  • RNN에 Batch Normalization을 적용할 때에는 매 time-step마다 다른 통계량을 계산하고 저장해야 한다. 이는 test sequence가 train 문장들보다 길 때 통계량을 이용할 수 없다는 문제가 있다.

Layer Normalization은 현재 time-step에서 특정 layer로 들어오는 summed input에 의존하기 때문이다.(+ 모든 time-step에 대해서 한 쌍의 gain과 bias parameter만을 가진다.)

Analysis

Invariance under weights and data transformations

layer normalization, batch normalization, weight normalization의 공통점

• 3개의 정규화 스칼라값은 계산방법이 다르지만, 3가지 방법 다 뉴런으로 들어온 summed input을 μ 와 σ, 두개의 스칼라로 정규화 한다.
• 각 뉴런에서 정규화 이후에 adaptive bias와 gain을 학습한다.

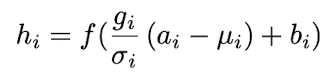
Weight re-scaling and re-centering

• batch Normalization 과 weight Normalization

  • incoming weight wi에 대한 re-scaling이 정규화된 input에 영향을 주지 않는다.

  • weight vector가 δ로 re-scaling되면, μ, σ 역시 δ 만큼 scaling 된다.
  • 다시말해, 가중치의 re-scaling에 invariant하다.

• Layer Normalization

  • 단일 weight vector의 re-scaling에 대해 invariant 하지 않다.
  • 대신에, 전체 weight matrix의 scaling과 incoming weight matrix의 shift에 대해 invariant 하다.

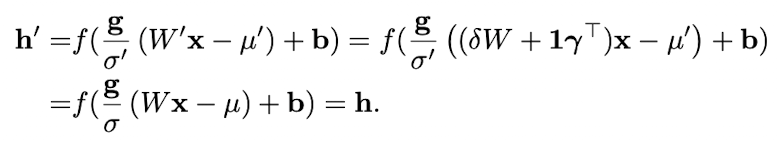
(만약 normalization이 weight 이전의 input에게만 적용된다면, model은 re-scaling과 re-centering에 대해 invariant 하지 않다.)

• W : 기존 weight matrix
• W′: W를 δ만큼 scale, γ만큼 shift한 weight matrix

Data re-scaling and re-centering

• batch Normalization 과 weight Normalization
  • dataset의 re-scaling에 대해 invariant 하다.
  • 뉴런에 전해지는 summed input 들이 변하지 않는다.
• Layer Normalization
  • dataset의 re-scaling에 대해 invariant 하다.
  • 각각의 training case들의 re-scaling에 대해 invariant 하다.
  • μ, σ가 현재의 input data에만 의존하기 때문이다.

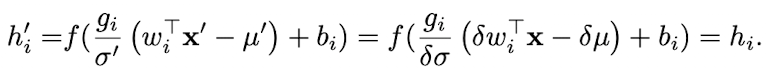
• X : 기존 data
• X’: X를 δ만큼 re-scaling한 data

Geometry of parameter space during learning

매개변수 공간의 기하학과 manifold를 통해 learning behavior를 분석한다.

= 기하학을 통해 정규화가 학습을 안정화 시키는것을 분석.

Riemannian metric

확률 모델의 학습 가능한 parameter들은 모델의 모든 가능한 input-output 관계로 부드러운 manifold를 만든다.

출력이 확률 분포인 모델의 경우, 이 manifold에서 두 점의 분리를 측정하는 자연스러운 방법은 모델 출력 분포 사이의 kullback-Leibler 발산이다.

이 발산 metric에서, 매개변수 공간은 reimannian manofold이다.

riemannian metric에 의해 riemannian manifold의 곡률은 ds^2 로 표현된다.

이는 매개변수 공간의 점에서 접선 공간의 최소 거리로, 접선 방향을 따라 매개변수 공간에서 출력되는 모델의 변화를 측정한다.

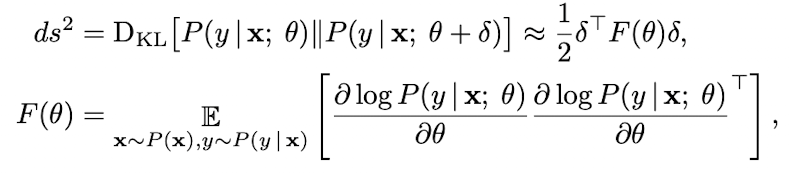
• δ : parameter의 작은 변화

위에 보이는 식(Riemannian metric)은 정규화 방법들이 어떻게 neural network training에 도움을 줄 지에 대한 통찰력을 제공한다.

The geometry of normalized generalized linear models

다음 분석의 결과는 각 블록이 단일 뉴런에 대한 parameter에 해당하는 fisher information matrixd에 대해 block diagonal approximation(블록 대각 근사치)을 갖는 neural network를 이해하는데 쉽게 적용될 수 있다.

Generalized linear model(GLM) 은 가중치 벡터 w와 bias scalar b를 사용하여 지수족(exponential family)의 출력 분포를 매개변수화 하는 것으로 간주할 수 있다.

GLM의 log likelihood는 summed inputs a 를 활용해 다음과 같이 쓸 수 있다.

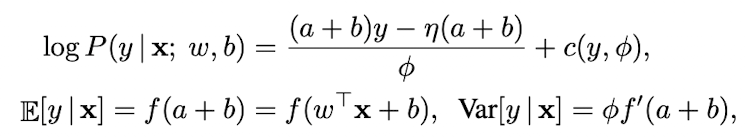
• f(·) : neural network의 non-linearitydㅘ 유사한 전달함수
• f’(·): 전달함수의 도함수
• η(·) : 실수값 함수
• c(·) : log 분배함수
• φ : output variance 조절 상수

H차원의 출력벡터 y = [y1,y2,…,yh]가 H개의 독립적인 GLM들로 모델링되고,

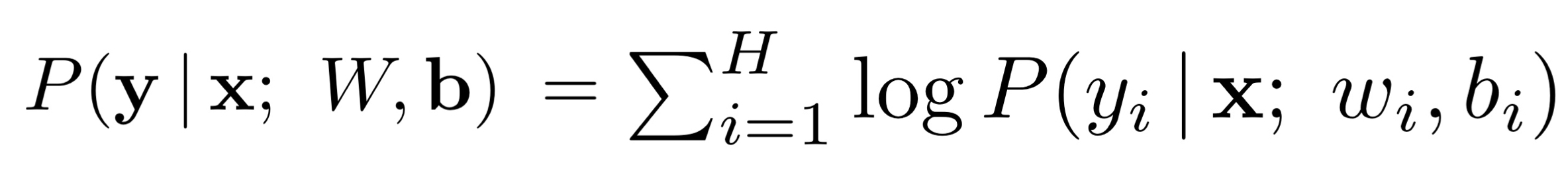
이라고 가정하고, weight matrix W의 각각의 열이 개별의 GLM들의 weight vector,b는 길이가 H인 bias vector이고 vec(·)는 Kronecker vector 연산자라고 하자.

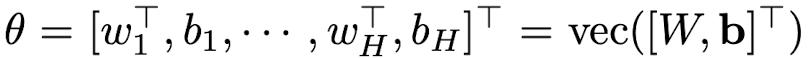
매개변수 θ에 대한 다차원 GLM의 Fisher information matrix는 단순히 데이터 feature와 출력 공분산 행렬의 expected Kronecker product 이다.

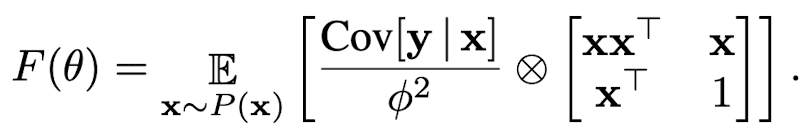
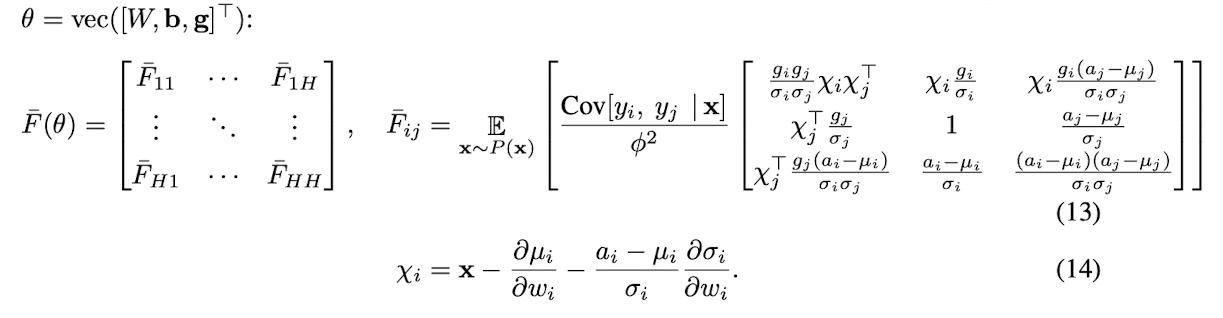
• μ and σ를 통해 원래 모델에서 summed input에서 a에 normalization method를 적용하여 normalized GLM을 얻는다.
• F bar :Fisher information matrix 로 나타낸 additional gain parameter θ를 가진 normalized multi-dimension GLM

Implicit learning rate reduction through the growth of the weight vector

wi 방향의 Fijbar는 gain 파라미터 g와 정규화 스칼라값 σi에 의해서 조정된다.

모델의 output이 동일하더라도 weight vector wi의 norm이 2배로 커지면 Fisher information matrix가 달라진다.

σi가 2배 더 커지기 때문에 wi방향의 곡률은 1/2만큼 변화한다.

결과적으로 정규화된 모델에서 동일한 parameter update에 대해 weight vector의 norm은 효과적으로 weight vector의 learning rate를 조절한다.

따라서 정규화 방법은 weight vector에 early stopping 효과를 가져오며 수렴을 위한 학습을 안정화 하는데 도움이 된다.